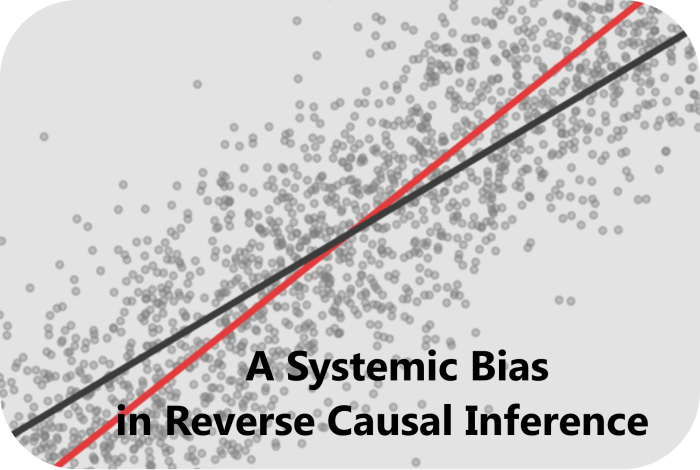
回归模型通常并不研究变量间的因果关系,而是仅估计特征和目标变量之间的相关关系。然而,当我们试图沿着数据生成过程的反方向进行回归分析时会引入一个系统性的估计偏差。这种偏差形式上类似于衰减偏差,即回归系数被系统性低估,但其成因是回归方向与因果结构不一致,而非测量误差。本文旨在用简单数学推导证明有偏估计量总是在逆数据生成过程的回归分析中出现,并对此展示了一种可以调整该偏差量的方法。
Category Archives: Traditional Machine Learning
Shall we worry about current AI taking over the world?
The recent spotlight on large language models (LLMs, such as Chatgpt) seems to have divided the public into two parties, debating whether they will take over human governance and control the world in the coming era of artificial intelligence, or whether they simply are tools to boost our productivity. What we should expect and what we could do in the right way to create reliable, trustworthy and safe AI?
Learning Record: Causal Inference [2]
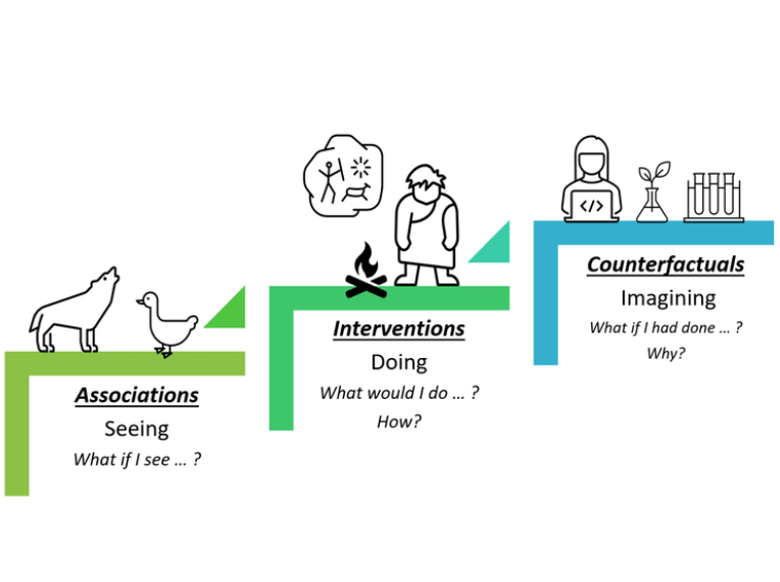
RCT may not be feasible all the time. But does it mean that we are just stuck in the first step of Pearl’s causal ladder? This blog introduces two fundamental methods Backdoor and Front-door Adjustment that can be used to answer interventional and counterfactual queries (the 2nd and 3rd steps in Pearl’s causal ladder) if the causal relationship satisfies certain criteria.
Learning Record: Causal Inference [1]
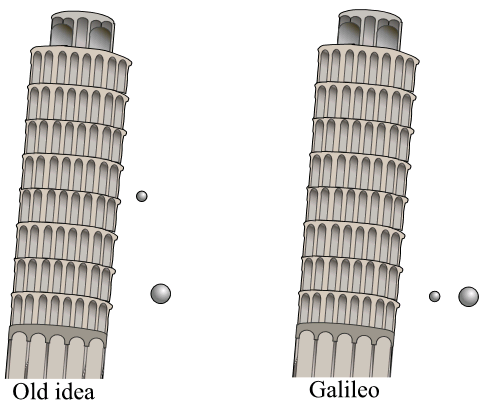
Correlation, or so-called associational relationship, absolutely should never imply the causation, while it is quite common for even some professional statistists to make this mistake. In fact, the debate between correlation and causation has persisted decades: A part of classical statistists, such as Francis Galton and Karl Pearson, insisted that causation is an “anti-scientific” subject. As a result, related exploration was stalled for many years, and some exciting and gratifying advancements are observed still very recent years.
New Trends in the Electricity Systems: Embracing Artificial Intelligence
This blog mainly aims to discover the potentials and ethical implications of applying machine learning techniques to electricity systems and introduces some pioneers who successfully integrate machine learning techniques to improve the electricity system effectiveness and efficiency.
浅谈回归(Regression)- [2]
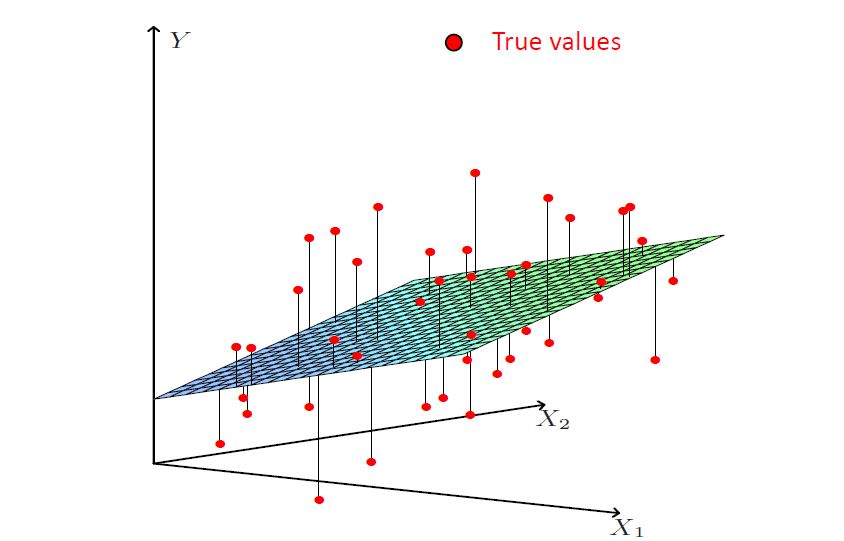
线性回归模型作为一种被深入研究并且已经广泛应用的数理模型,具有可解释性强、计算复杂度低、适合处理大量数据等优势。其中,普通最小二乘法(Ordinary Least Squares, OLS)则是对线性回归模型进行参数估计的主流方法。相关的研究已经严格地证明,在满足若干基本假设的前提下,普通最小二乘估计量(OLS Estimators)就是线性回归模型的最佳无偏估计量(Best Linear Unbiased Estimator, BLUE)。
浅谈回归(Regression) – [1]
回归(Regression)作为监督学习能解决的两大问题之一,是一类基于统计的预测问题的统称,可以使用的模型也多种多样,如线性回归、Polynomial回归、逻辑回归、Softmax回归。其中线性回归和逻辑回归最广为人知,因为它们不仅是广大商科同学在计量经济学中的主要学习内容,而且也已广泛地被各种机器学习课程作为入门模型进行介绍。