反向回归中OLS估计的系统性偏差

——一个总是被忽视的偏差

回归模型通常并不研究变量间的因果关系（causation)，而是仅估计特征和目标变量之间的相关关系（correlation）。然而，当我们试图沿着数据生成过程的反方向进行回归分析时（例如数据生成过程为 $Y \rightarrow X$ 却用 $X$ 回归 $Y$ ，即建模 $\hat y = f(x)$ ），会引入一个系统性的估计偏差。这种偏差形式上类似于衰减偏差（Attenuation Bias），即回归系数被系统性低估，但其成因是回归方向与因果结构不一致，而非测量误差。本文旨在用简单数学推导证明有偏估计量总是在逆数据生成过程的回归分析中出现，并对此展示了一种可以调整该偏差量的方法。

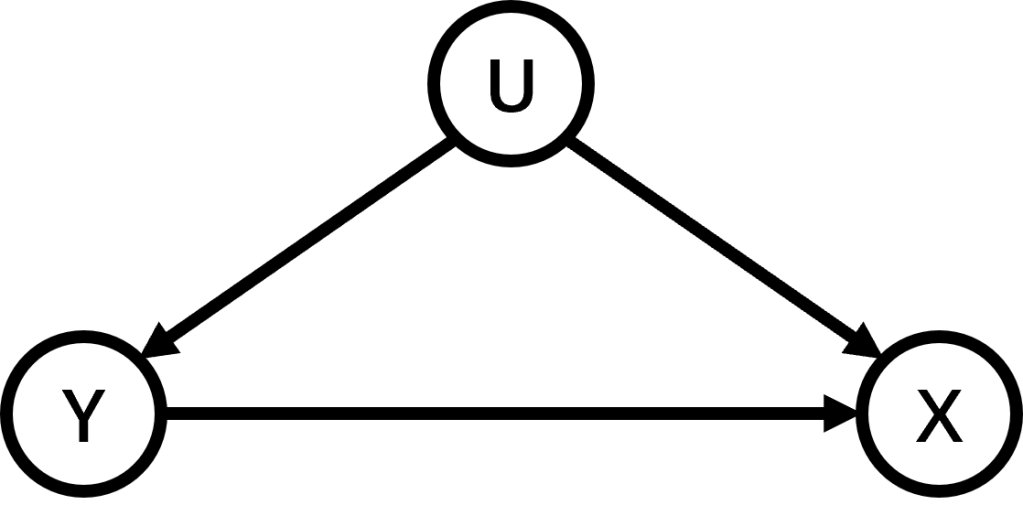
在医学诊断领域，我们常常需要做所谓的反向因果推断（reverse causal inference)。例如图1.中所展示的一个前门混杂因果模型， $Y$ 可以是某种疾病潜在风险程度， $X$ 则可以是对潜在患病人群的某些医学指标的观测结果， $U$ 可以是一些可以被认为是原因变量 $Y$ 和结果变量 $X$ 共同原因的混杂因子（例如环境因素、年龄等等）。通过例如RCT之类的金标准实验设计框架，如果我们真的全面且正确地控制了混淆因子，我们的确可以拿到不受混杂因子 $U$ 影响的“良好”数据，反应了 $Y$ 和 $X$ 之间的真实因果关系。实际诊断中，我们常常需要使用我们观测到的医学指标，对潜在患者的该项疾病风险做出评估。即从结果变量 $X$ 预测原因变量 $Y$ 。

图1. 一个前门混杂的因果图例子，其中原因变量为 $Y$ ，结果变量为为 $X$ ，混杂因子为 $U$ 。在此例中，结果变量 $X$ 的观测由 $U$ 和 $Y$ 共同生成。

按照图1.中的模型，我们可以假设从原因 $Y$ 到结果 $X$ 的直接因果关系为：

$X=\alpha_{1}Y+\alpha_{0}+\zeta$

其中， $\zeta$ 是一个方差为 $\sigma_{\zeta}^{2}$ 的独立随机误差项。当我们想要建立一个利用 $X$ 预测 $\hat{Y}$ 的回归模型（反向因果推断）时，该回归模型可以表示如下：

$\hat{Y}=\hat{\beta_{1}}X+\hat{\beta_{0}}+\epsilon$

其中， $\epsilon$ 是残差项。记变量 $Y$ 和 $U$ 的方差为 $\sigma_{Y}^{2}$ 及 $\sigma_{U}^{2}$ ， $X$ 和 $Y$ 的协方差为 $\sigma_{XY}$ 。理论上来说，我们期望 $\alpha_{1}$ 和 $\beta_{1}$ 应互为倒数关系，因为他们确实都是描述 $X$ 和 $Y$ 之间关系大小的系数，即：

$\hat{\beta_{1}}=\frac{1}{\alpha_{1}}$

现在让我们来分析一下，OLS估计下， $\hat{\beta_{1}}$ 是否真的是 $\alpha_{1}$ 的倒数呢？OLS估计给出的 $\hat{\beta_{1}}$ 可以表示如下：

$\hat{\beta_{1}}=\frac{\sigma_{XY}}{\sigma_{X}^{2}}$

接下来，让我们分别计算上式的分子和分母。其中，由于随机误差项 $\zeta$ 与 $Y$ 独立，即 $\zeta\perp Y$ ， $X$ 和 $Y$ 的协方差 $\sigma_{XY}$ 为：

$\begin{alignedat}{1}\sigma_{XY} & =\mathrm{Cov}\left(\alpha_{1}Y+\alpha_{0}+\zeta,Y\right)\\ & =\mathrm{Cov}\left(\alpha_{1}Y,Y\right)\\ & =\alpha_{1}\sigma_{Y}^{2} \end{alignedat}$

同时，分母 $X$ 的方差 $\sigma_{X}^{2}$ ：

$\begin{alignedat}{1}\sigma_{X}^{2} & =\mathrm{Var}\left(\alpha_{1}Y+\alpha_{0}+\zeta\right)\\ & =\alpha_{1}^{2}\sigma_{Y}^{2}+\sigma_{\zeta}^{2} \end{alignedat}$

将上面计算的 $\sigma_{X}^{2}$ 和 $\sigma_{XY}$ 代入到OLS估计量 $\hat{\beta_{1}}$ 的表达式中，可以得到：

$\begin{alignedat}{1}\hat{\beta_{1}} & =\frac{\alpha_{1}\sigma_{Y}^{2}}{\alpha_{1}^{2}\sigma_{Y}^{2}+\sigma_{\zeta}^{2}}\\& =\frac{1}{\alpha_{1}}\frac{\sigma_{Y}^{2}}{\sigma_{Y}^{2}+\left(\frac{\sigma_{\zeta}}{\alpha_{1}}\right)^{2}} \end{alignedat}$

可以从上式中看出， $\hat{\beta_{1}}$ 并不总等于 $\frac{1}{\alpha_{1}}$ ，而是还需要在它的基础上乘以一个总是小于等于1的系数 $\frac{\sigma_{Y}^{2}}{\sigma_{Y}^{2}+\left(\frac{\sigma_{\zeta}}{\alpha_{1}}\right)^{2}} \leq 1$ 。因而，这样反因果推断回归得到的系数总是有偏的，而且总是会偏小。

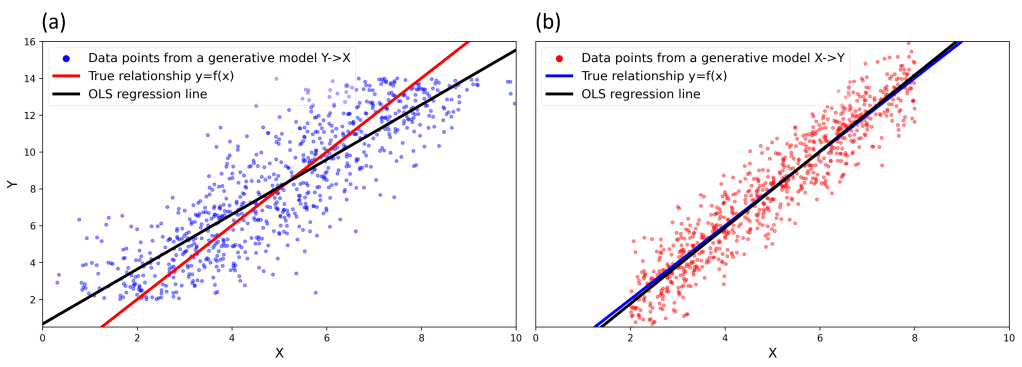
图2. (a)具象化地展示了这种偏差。在图2. (a)中， $X$ 是由 $Y$ 生成的，红色线表示这两个变量间真实的关系，也即 $Y=\frac{1}{\alpha_{1}}X-\text{\ensuremath{\frac{\alpha_{0}}{\alpha_{1}}}}+\zeta'$ 。而OLS回归模型由黑色线表示，它的斜率（即 $\hat{\beta_{1}}$ 明显小于 $\frac{1}{\alpha_{1}}$ ，是一个前文证明的系统性偏差。而在图2. (b)这个由 $X$ 生成 $Y$ 的生成顺序下， $Y$ 对 $X$ 的OLS回归并没有此项系统性偏差。

图2. 分别展示对比了两种数据生成顺序的样本分布和 $X$ 和 $Y$ 的真实关系，以及在各自数据样本上的OLS回归模型。其中，(a)是由 $Y$ 生成 $X$ ，红线表示生成关系，也即两个变量间的真实关系，而黑线则代表在此生成模型下 $Y$ 对 $X$ 的OLS回归。正如前文所试图证明的，这里的OLS回归相对真实生成关系来说是有偏的。相反地，(b)是由 $X$ 生成 $Y$ ，红线表示生成关系，也即两个变量间的真实关系，而黑线则代表在此生成模型下 $Y$ 对 $X$ 的OLS回归，而这里的OLS回归相对真实关系来说是无偏的。

在实际的反向因果推断中，我们并不能明确的知道生成过程的具体参数，那么我们又该如何估计去除掉这个系统性偏差的真实关系呢？让我们尝试从反向因果推断的回归模型 $\hat{Y} =f\left(x\right)$ 的残差项 $\epsilon$ 入手：

$\epsilon_{i}=y_{i}-\hat{\beta_{1}}x_{i}$

然后，我们可以估计它的方差 $\hat{\sigma}_{\epsilon}^{2}$ ：

$\begin{alignedat}{1}\hat{\sigma}_{\epsilon}^{2} & =\mathrm{Var\left(Y\hat{\beta_{1}}\left(\alpha_{1}Y+\alpha_{0}+\zeta\right)\right)}\\& =\mathrm{Var}\left(\left(1-\hat{\beta_{1}}\alpha_{1}\right)Y-\hat{\beta_{1}}\alpha_{0}-\hat{\beta_{1}}\zeta\right)\\& =\left(1-\hat{\beta_{1}}\alpha_{1}\right)^{2}\sigma_{Y}^{2}+\hat{\beta}_{1}^{2}\sigma_{\zeta}^{2} \end{alignedat}$

联立这个残差项的方差表达式和上文给出的有偏OLS估计 $\hat{\beta_{1}}$ 的表达式：在样本量足够大的情况下，我们可以明确知道 $\hat{\beta_{1}}$ , $\hat{\sigma}_{\epsilon}^{2}$ 以及 $\sigma_{Y}^{2}$ （其中， $\hat{\sigma}_{Y}^{2}\xrightarrow{a.s.}\sigma_{Y}^{2}$ ）的值。我们可以通过这两个方程解出 $\alpha_{1}$ 以及 $\sigma_{\zeta}^{2}$ 这两个未知数。据此，我们所关心的 $Y$ 和 $X$ 之间的真实关系就可以被无偏地描述。