Learning Record: Causal Inference [2]

Posted byjianqiaomaoPosted inBlogs, Learning Records, Original Articles, Traditional Machine LearningTags:,
Two Scenarios: Backdoor and Front-door Adjustment

Main learning materials and reference:
[1] Pearl, Judea. Causality. Cambridge university press, 2009.
[2] Introduction to Causal Inference by Brady Neal,.

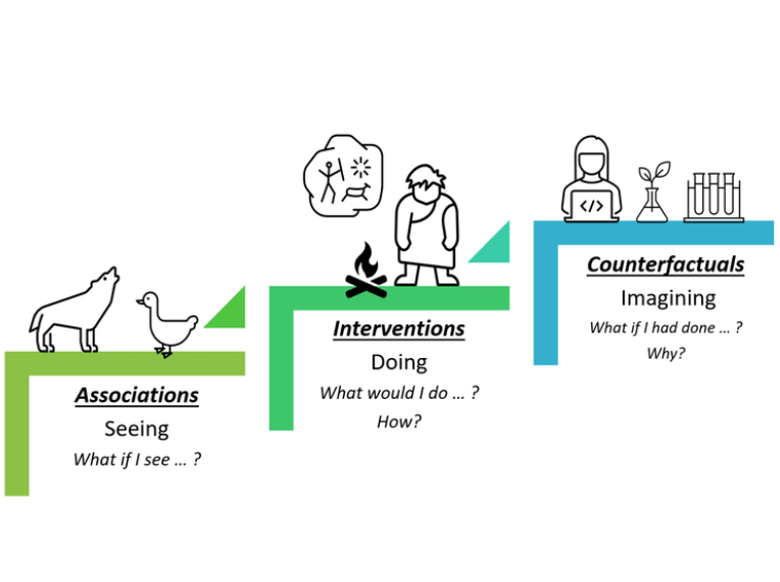
In the last blog, we demonstrated that correlation is not causation, except when it is. Although the difference between correlation and causation is what we would like readers to take home, the second clause, sometimes, is more important. In the example of conducting Randomised Control Trail (RCT), we tried to convince you that RCT can always guarantee that the treatment is independent from the existing known confounders. In this case, correlation also implies causation. Unfortunatly, RCT may not be feasible all the time. For instance, it is unethical to enforce non-smoker to smoke when investigating the causal effect between smoking and lung cancer. But does it mean that we are just stuck in the first step of Pearl’s causal ladder [1]?

The answer is NO. Thanks to Pearl’s thoughts, do-calculus can help us continue to climb the ladder. Let’s go back to the example of “if sleeping with shoes on will lead to headache?” illustrated in last blog (Fig. 1). What RCT actually does here is to ensure the treatment (T) to be independent from the the confounder (X), that is T \perp \!\!\! \perp X. In Pearl’s causal language, the RCT blocks the causal path from the drunk state to shoes-on state.

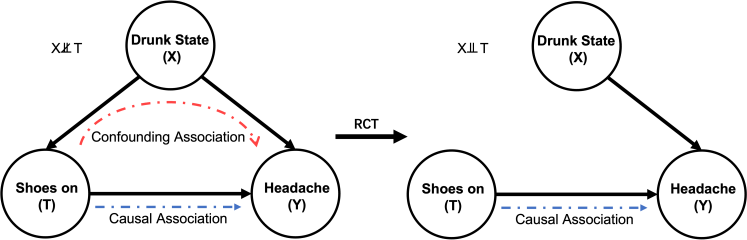
Fig. 1 Will sleeping with shoes on make you headahe?
(Source: https://www.bradyneal.com/causal-inference-course)
Backdoor Adjustment

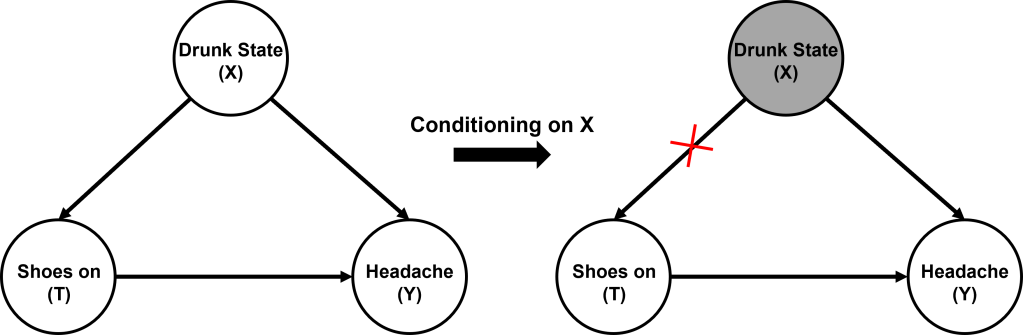
In fact, there is another way to block the path, that is, condition on the counfounder (X) and then do marginalisation. This is equivalent to sub-grouping experimental subjects based on all the covariants and study the effect of a given treatment in RCT. Mathematically, the interventional probability of headache (Y) can be expressed as follow:

P(y|do(T = t)) = \sum\nolimits_x {P(y|do(T = t),x) \cdot P(x|do(T = t))}

Since conditioning on the X, we block all the non-causal paths from T to Y, then the causal effect of T to Y is just the correlation, which means P(y|do(T = t),x) = P(y|t,x) . And because we intervene on T (do(T=t) ) no matter what X is, do(T=t) should be independent from X, that is do(T=t) \bot X . Therefore, the above interventional probability can be re-written as:

P(y|do(T = t)) = \sum\nolimits_x {P(y|t,x) \cdot P(x)}

This is the so-called Backdoor Adjustment, and Fig.2 is its graphical representation.

Fig. 2 The structural causal model for Backdoor Adjustment
Front-door Adjustment

Importantly, this adjustment method is only valid when the confounder X is a sufficient adjustment set and is also known. However, real-world problems are always more complex, for example, let’s think about a scenario, where we are not able to measure confounders or we just don’t know what confounders are, and there is a mediator factor between the cause and effect. The real-world instance might be the causal effects between smoking and getting lung cancer shown in Fig.3. Let’s assume the treatment is smoking (T), and the mediator is the quantity of tar left in the lung (M), the effect is lung cancer (Y) and a set of unmeasurable and unknown confounders (U) exist. For instance, the unknown confounders could be a gene that can increase the intention of smoking and the risk of lung cancer at the same time.

Fig. 3 The structural causal model of smoking and lung cancer

RCT is unethical in this scenario, but we really need to infer to what extent smoking can lead to lung cancer. Backdoor adjustment is invalid in this case, because the unknown factors are not measurable. A possible way is to use Front-door Adjustment. To understand Front-door Adjustment, we try to measure the causal effect from T to Y (P(y|do(T = t)) ) in two steps, where the first step identifies the causal effect from T to M (P(m|do(T = t)) ) and the second step identifies the causal effect from M to Y (P(y|do(M = m)) ). Formally, we can express it as:

P(y|do(T = t)) = \sum\nolimits_m {P(m|do(T = t)) \cdot } P(y|do(M = m))

For step 1, since Y acts as a collider that naturally blocks causal paths from T to Y except the one via mediator M, the interventional probability is just the conditional probability of m given t:

P(m|do(T = t)) = P(m|t)

For step 2, we apply Backdoor Adjustment by blocking the only non-causal path from M to Y via T and U. Specifically, the treatment T is a sufficient adjustment set here. Therefore, we have:

P(y|do(M = m)) = \sum\nolimits_t {P(y|m,t) \cdot P(t)}

Now, we can derive the interventional probability of Y given do(T=t) :

P(y|do(T = t)) = \sum\nolimits_m {P(m|t) \cdot } \sum\nolimits_{t'} {P(y|m,t') \cdot P(t')}

Fig. 4 The structural causal model for Front-door Adjustment

Last but not the least, we may formally state the criterion for both Backdoor Adjustment and Front-door Adjustment to notify when we can use the two simple but vital methods for a given structural causal model.

Backdoor Adjustment Criteria

A set of variables W satisfies the backdoor criterion to T and Y if:

  • W blocks all backdoor paths from T to Y
  • W does not contain any decendants of T
Front-door Adjustment Criteria

A set of variables M satisfies the front door criterion to T and Y if:

  • M completely mediates the effect of T and Y
  • There is no unblocked backdoor path from T to M

As we have all seen, these criteria are quite strict, which may not suit all possible structural causal models. Therefore, we may need a more generalised toolset that can help us deal with more complicated causal graphs (if the causal effect is identifiable). In a later blog of Learning Record: Causal Inference, we may discuss Do-calculus, a powerful tool that can deal with arbitrary identifiable causal effects.

In conclusion, this blog introduces two fundamental methods Backdoor and Front-door Adjustment that can be used to answer interventional and counterfactual queries (the 2nd and 3rd steps in Pearl’s causal ladder) if the causal relationship satisfies certain criteria.

Leave a comment