浅谈回归（Regression）- [2]

——基于OLS的线性回归模型参数估计

线性回归模型作为一种被深入研究并且已经广泛应用的数理模型，具有可解释性强、计算复杂度低、适合处理大量数据等优势。其中，普通最小二乘法（Ordinary Least Squares, OLS）则是对线性回归模型进行参数估计的主流方法。相关的研究已经严格地证明，在满足若干基本假设的前提下，普通最小二乘估计量（OLS Estimators）就是线性回归模型的最佳无偏估计量（Best Linear Unbiased Estimator, BLUE）。

回顾上篇，我们如果想找到一个方法对狗剩所“盘算”的预测未来收入的一元线性回归模型进行评估，一个最凭直觉的标准就是衡量狗剩所拟合的直线和所有样本点的距离远近——一个好的模型应当能让所有样本点到直线距离的总和尽量地小，而差的模型这个距离总和则会比较大。图1. a) 和 b)能直观地展现这一点：

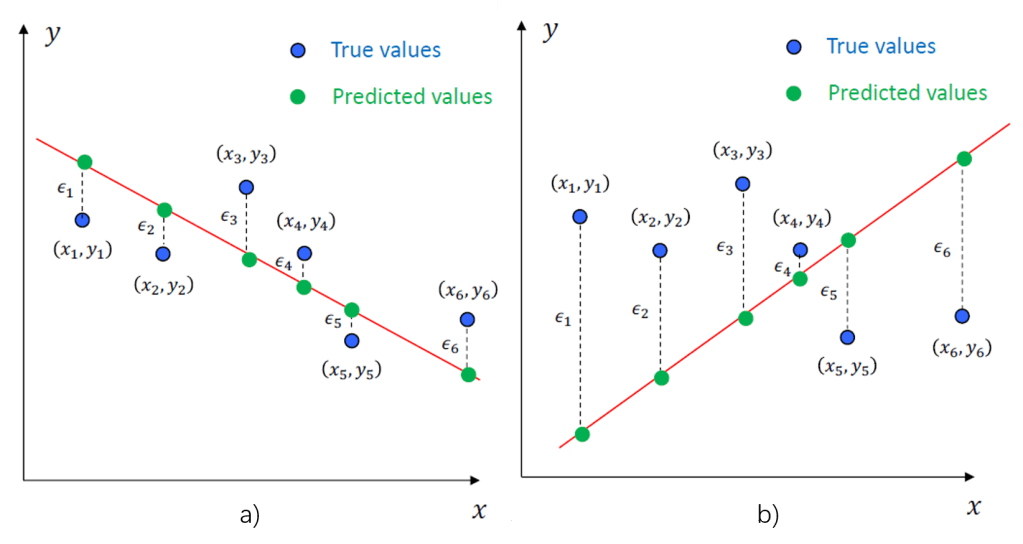
图中，对于每一个样本点 $({x_i},{y_i}), i=1,2,..., 6$ ，样本的真值 $y_i$ 和模型预测值 ${\hat y_i}$ 的差反应了实际观测值和拟合值的差异，被称为残差（Residual） $\varepsilon_i$ 。但要注意到直接利用残差和评估模型优劣是不合理的，因为残差有正有负，直接相加导致的正负相消使得残差和并不能反映所有样本点到直线的总距离。因此，这里需要对残差取绝对值后求和，即总距离应该被表示为:

$\begin{array}{l} D = \sum\limits_i {|{\varepsilon _{_i}}|} \\ \quad \ = \sum\limits_i {|{y_i} - {{\hat y}_i}|} \\ \quad \ = \sum\limits_i {|{y_i} - ({\hat \beta _0} + {\hat \beta _1} \cdot {x_i})|} \end{array}$

至此，可以说一个 $D$ 越小的线性回归模型，对于观测值的拟合程度就越好，模型也就越好。与此同时，可以发现这个对于模型好坏的评价标准也为我们提供了一种寻找好模型的思路，即找到一组最优的模型参数： $\beta^* = \{ {{ \beta^* }_0},{{ \beta^* }_1} \}$ 使得D的值能尽量小，表示为：

${\beta ^*} = \mathop {\arg }\limits_{\hat \beta } \min \{ \sum\limits_i {|{y_i} - ({{\hat \beta }_0} + {{\hat \beta }_1} \cdot {x_i})|} \}$

但是，要直接解决这样的一个带有绝对值的目标函数是比较困难的，因为其并不处处可导的。一种比较好的替代办法是对 $|{y_i} - ({{\hat \beta }_0} + {{\hat \beta }_1} \cdot {x_i})|$ 取平方，这样做既不改变原目标函数的凹凸性（严格下凸），也不改变最优解的取值。因此可以用残差的平方和(RSS)来定义一个新的对模型优劣的评价函数（或损失函数） $loss(RSS) = \sum\limits_i {{{({y_i} - {{\hat y}_i})}^2}}$ 。这样，要解决的最优化问题变为：

${\beta ^*} = \mathop {\arg }\limits_{\hat \beta } \min { \sum\limits_i {{{[{y_i} - ({{\hat \beta }_0} + {{\hat \beta }_1} \cdot {x_i})]}^2}} }$

对于这样一个高中阶段就可以处理的凸优化问题，只需要分别计算使得 $loss$ 对 ${\hat \beta }_0, {\hat \beta }_1$ 的偏导等于0时的 ${ \beta^* }_0,{ \beta^* }_1$ 就行了，即计算：

$\begin{array}{l} \frac{{\partial loss}}{{\partial {{\hat \beta }_0}}} = 0\ \\ \\ \frac{{\partial loss}}{{\partial {{\hat \beta }_1}}} = 0 \end{array}$

进一步地，可以得到 ${ \beta^* }_0,{ \beta^* }_1$ 的表达式如下：

${{\hat \beta }_1}^*{\rm{ = }}\frac{{\sum\limits_i {{x_i}({y_i} - \bar y)} }}{{\sum\limits_i {{x_i}({x_i} - \bar x)} }} \\ {{\hat \beta }_0}^*= \bar y - {{\hat \beta }_1}^* \cdot {\bar x}$

至此，我们就获得了一个残差平方和最小的模型。当模型的参数被估计后，一般需要考虑它的优劣性，即它是否能代表总体参数的真实值。高斯-马尔科夫定理（Gauss-Markov Theorem）已经说明，在经典线性回归的基本假设全部满足的情况下，OLS估计所得到的的估计量是具有最小方差的线性无偏估计量。关于经典线性回归的基本假设，本文由于篇幅有限就不做展开，但对于感兴趣的读者或者正在学习计量经济学的同学，这些假定至关重要——对于不满足基本假定的模型如何检验及如何修正。

比较有趣的一点是进一步探索RSS的含义。基于前面的分析，我们似乎已经解决了全部的问题：指定了评价模型优劣的一般性标准并且找到了能够使得RSS最小的一组模型参数 $\beta^*$ 。但是，当狗剩拿着他找到的最优模型去劝说和他一起入职的隔壁老王一起跳槽时，老王问了一句“这模型，有多好？”。因此，问题的关键在于，狗剩敢于保证他找到的模型是基于这些观测值最好的一个，但是仍然无法回答“他的模型有多好”这个问题。因为RSS并不是一个相对量，对于同样的一组同事的收入和工龄观测值，如果狗剩利用美元和人民币两种货币单位对收入进行衡量，那么这两个模型的拟合优劣应当时一致的，但是明显地，从数值上来看，以美元为计价货币的模型的RSS($^2)将比以人民币为计价货币的模型的RSS(￥^2)低很多！

因此如果我们能找到观测值的浮动（方差）中有多少部分可以被回归模型所解释，就可以以一种更公平地方式评价一个回归模型有多好。很直观地，RSS实际上就是回归模型所不能解释的那部分浮动（方差），而观测值总的方差实际上就是观测值整体的浮动，他们的比值就反应了这些观测值的浮动有多少部分是不能被回归模型解释的。相对地，也就知道了多少部分是能被回归模型解释的。更严谨地，可以定义总体平方和（TSS）为 $TSS = \sum\limits_i {{{({y_i} - \bar y)}^2}}$ ，而拟合优度 ${R^2}=1- \frac{RSS}{TSS}$ ，是一个介于0到1的值。图2直观地展现了一个回归模型总方差的构成关系。

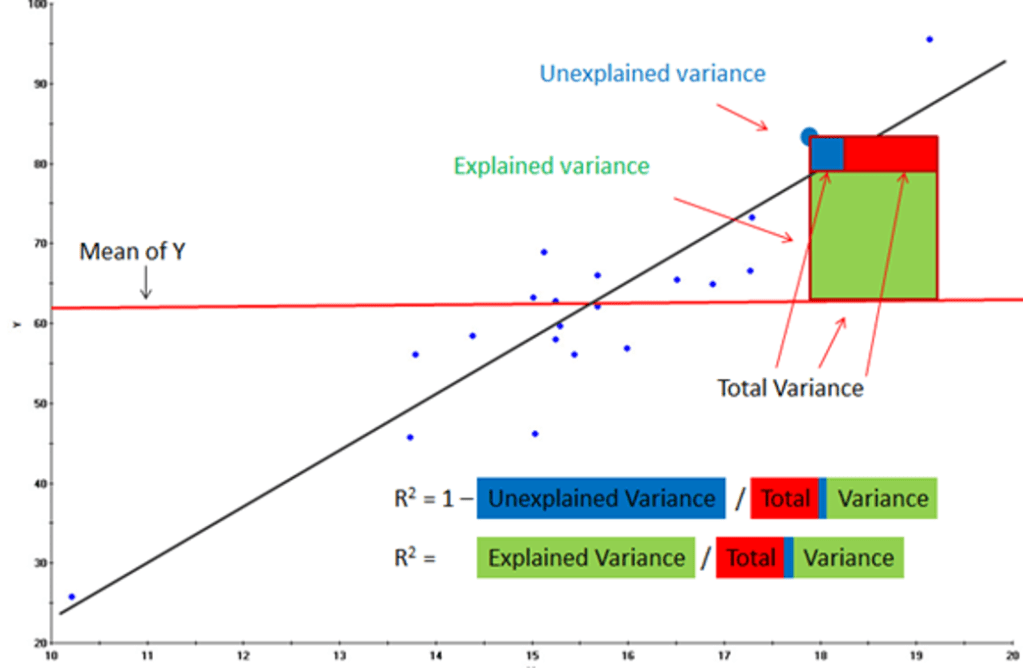
终于，狗剩利用这种方法在计算出它的模型的拟合优度 ${R^2}$ 后，自信地又跑去找了老王。老王看了几眼，说（唱）到“我们不一样，每一个人都有不同的境遇。”，于是拿出了自己MIT本硕博的学位证，“老板说下个月给我加薪呢。”。正如上一篇文章所分析的那样，除了工龄，学历、业绩、周工时等等因素也应该会对未来的收入水平有所影响。所以，狗剩要想更准确地估计未来收入，则必须要考虑到上述的除工龄外的一个或多个变量。于是，狗剩又坐不住了，跑去把那些被他骚扰过的同事们又调查了一遍，决定盘算一个可以考虑多个自变量的多元线性回归模型。

图3展示了一个有两个自变量的多元线性回归模型。需要注意的是，在这样一个三维空间里，模型的几何表示不再是一条直线，而变成了一个二维平面，观测值和预测值的距离则应当是观测值到回归平面的距离。可以发现，这已经是多元回归模型能可视化展示的极限——对于有三个自变量的多元回归模型，其回归模型的几何表示将成为一个在四维空间中的超平面（体）。

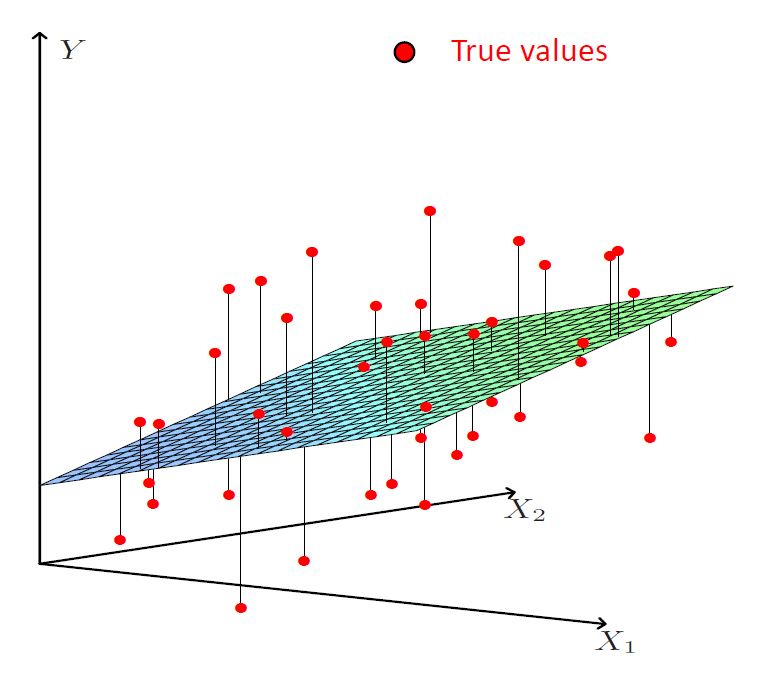
有了上面一元线性回归模型的评价方法和参数估计的基础，要进一步探究多元线性回归，我们只需在其基础上推广到具有多个自变量时即可。类似地，多元线性回归模型可以被表示为：

${\hat {y_i}} = {\beta_0} + {\beta_1}{x_{i,1}} + {\beta_2}{x_{i,2}} +... + {\beta_m}{x_{i,m}}$

对于上式中的样本点 ${\bf {x_i}}$ ，可以表示为向量形式： ${\bf {x_i}} = {[1,{x_{i,1}},{x_{i,2}},...,{x_{i,m}}]}$ ， ${R^{1 \times m}}$ ，向量中的元素分别代表着工龄、学历、周工时等影响收入的因素。而模型参数 ${\bf B}$ ， ${R^{m \times 1}}$ ，可以被表示为 ${\bf B} = {[{\beta_0},{\beta_1},...,{\beta_m}]^T}$ ，向量中每个元素分别代表着其对应的影响收入的因素的权重。注意到这里的样本向量 ${\bf {x_i}}$ 的第一个元素为1，目的是构造一个有截距项 ${\beta_0}$ 的模型。通常来说，在没有强有力的理论证明该模型不应包含截距项时，都应该预设截距项存在，否则会引起比较严重的模型设定偏误。因此，模型对样本向量 ${\bf {x_i}}$ 的预测值（即模型预测出来的某位同事的收入） ${\hat {y_i}}$ 应为 ${\hat {y_i}}= {\bf {x_i}} \bf B$ 。进一步的，对于所有的样本，多元线性回归模型的一系列输出 ${\bf{\hat y}} = {[{\hat {y_1}},{\hat {y_2}},...,{\hat {y_n}}]^T}$ ， ${R^{n \times 1}}$ 则可以被表示为：

$\hat{\boldsymbol{y}} = \boldsymbol{X} \hat{\boldsymbol{B}}$

同样地，利用RSS构造损失函数 $loss = RSS({\bf{B}}) = tr(({\bf{y}} - {\bf{\hat y}}){({\bf{y}} - {\bf{\hat y}})^T})$ ，其中 ${\bf{y}}$ 是真实的观测值（同事们的实际收入）。要获取最优的一组参数 ${\bf B^*}$ ，同样只利用偏导数等于零来解决损失函数最小化的问题就可以了。据此，可以解出最优的模型参数 ${\bf B^*} = {({{\bf{X}}^T}{\bf{X}})^{ - 1}}{{\bf{X}}^T}{\bf{y}}$ 。关于矩阵的求导规则，建议读者可以参考这个博客。

关于多元线性回归，一个值得讨论的问题是它的拟合优度 ${R^2}$ 。我们在利用 ${R^2}$ 评价多元线性回归模型的好坏时，要注意到它的一个性质： ${R^2}$ 是关于自变量个数的一个非减函数，即增加一个自变量 $x$ 时 ${R^2}$ 总是增大。这一点从拟合优度的定义就可以很好理解：

${R^2}=1- \frac{RSS}{TSS}$

显而易见地是，随着自变量数量的增加，RSS将会减小（至少是不变），这也就导致了 ${R^2}$ 也就随之增加。它暗含的一个问题是，这会导致模型评价时的不公平。例如，在狗剩预测收入这件事情上，仅仅用上述定义的拟合优度来比较仅包含工龄的模型和加入了多个其他自变量的模型的优劣，是不尽公平的，因为加入了更多自变量的模型几乎必然地有更高的拟合优度。另一方面，如果我们朴素地追求高的 ${R^2}$ ，而不顾一切地引入新的自变量，最终会引入过多的不相干变量。因此，一种通行的方式是，将拟合优度的大小根据自变量的数量进行调整：

${\bar R^2} = {1-(1-R^2)} \frac {n-1}{n-k}$

其中， $n$ 为观测样本的数量， $k$ 是模型中包括截距项在内的参数的个数（也就是自变量的个数+1）。 ${\bar R^2}$ 又被称为 ${R^2}$ ，它是对原拟合优度的定义式在自由度上的调整。

即使我们已经介绍了一元和多元线性回归这两种强大的统计分析方法，但是在实际应用中，因变量和某一些自变量的关系并不总只是线性的，所以它们仍然不能有效地解决自变量和因变量是非线性关系的问题。例如，狗剩喜欢吃苹果，吃一个苹果给他带来的满足度是10，而吃两个苹果给他带来的满足度是18，而你要给狗剩吃3个苹果，他的满足度可能只有20，因为他已经觉得开始撑了，吃到的第三个苹果并不能给狗剩带来和第一个苹果一样的快乐。这就是经济学上著名的边际效用递减规律。如果我们仍然利用吃苹果的数量 ${x}$ 作为自变量，对狗剩的满足度 ${y}$ 做前文提到的一元线性回归，可以预知这个线性回归模型的拟合程度将不尽人意。因此，我们或许可以对吃苹果的数量 ${x}$ 做一个变换，例如 ${log(x)}$ ， ${x^2}$ 等等，引入一些非线性的关系，更好地拟合回归模型。因此，下篇博客除了将介绍如何限制一般性的线性回归模型因过于复杂而导致过拟合以外，还将用一定的篇幅介绍Polynomial回归。