浅谈回归（Regression) – [1]

——从线性回归到逻辑回归

回归（Regression）作为监督学习能解决的两大问题之一，是一类基于统计的预测问题的统称，可以使用的模型也多种多样，如线性回归、Polynomial回归、逻辑回归、Softmax回归。其中线性回归和逻辑回归最广为人知，因为它们不仅是广大商科同学在计量经济学中的主要学习内容，而且也已广泛地被各种机器学习课程作为入门模型进行介绍。

在日常生活里，无论我们有没有意识到，我们多多少少都朴素地间接地使用了诸如线性回归、逻辑回归等回归模型解决实际问题。举个栗子，有一天刚入职的狗剩坐在他的小格子间上班摸鱼，心里盘算着自己十年以后能挣多少大洋。新来的狗剩只知道自己这个新人只能拿到微薄的3k薪水，但对其他同事的收入情况一无所知。狗剩心里疑惑，十年之后，他是能买得起一套深圳湾一号的海景房，还是只能像现在一样天天挤地铁到科技园上班？由于公司也才建立了八年，根本就没有在这供职时间达到十年的员工，很难直接了解十年工龄对应的收入水平。于是他只好打听了他们部门这八年间不同时间入职的同事们的收入，心里一盘算，发现在其他条件不变的情况下，平均来说，工龄每增加一年，同事们的收入就增长1k。狗剩在心里打了个草稿，又想了想深圳湾一号的梦想，第二天索性交了辞职信，去了隔壁公司上班。

狗剩这里的“盘算”，其实就是回归——他试图找到在他们公司（部门），工龄和收入这两个随机变量（Random Variable）之间的关系，并且利用这个关系，对自己未来的收入进行预测。

在狗剩的例子里，如果我们把他的“盘算”结果具象化为简单的一元线性回归模型，那它可以被表示为：

其中，被称为模型参数（parameter）。进一步地，可以将以上模型形象地表示为图1中的直线。而图中的红色十字点就是狗剩所调查的同事的工龄和收入这两个变量在这个直角坐标系中的表示，红圈所指示的正是刚入职的狗剩所处的境遇——月薪3k。那么狗剩所“盘算”的关键问题，就是如何寻找到这条最能描述他打听到的这些同事的工龄和收入关系的直线。

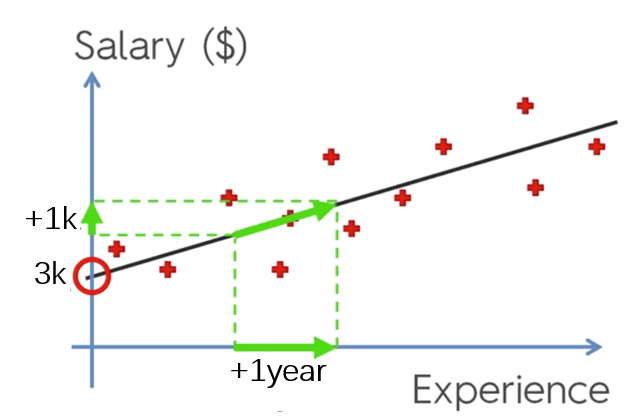
需要注意的是，回归分析仅仅探究了变量之间的依赖关系，分析的结果是一个统计关系式（模型），无论这个模型有多显著或具有多强的启发性，他都不能确立变量间的因果关系。事实上，因果关系是一个比相关关系更强的关系描述。换句话说，变量间具有相关性是变量间具有因果关系的必要不充分条件。要推论两个相关变量具有因果性，还需要很多其他条件来支撑，例如自变量的变化在时间上要先于因变量，模型本身在理论上要具有合理性等。在狗剩的例子里，如果单从模型的角度来看，其实很难断言是工资水平上升留住了员工还是工龄的增长牵动了工资上调。

当然，即使能证明工龄是牵动工资水平上涨的原因，狗剩的这个模型仍然是十分朴素的。实际上，影响狗剩同事收入的相关因素可能还有很多，例如学历、业绩、周工时等等。因此，仅凭工龄就寻求准确地预测未来收入，显然是不尽合理的。更准确地，我们应当在狗剩构建的模型的基础上，引入对收入水平也具有解释能力的一个或多个自变量，共同解释狗剩同事的工资水平。这类具有超过一个自变量的线性回归模型，被称为多元线性回归。进一步地，狗剩在预测了自己未来十年的收入水平后，进行是否要继续留在这家公司工作的决策时，他的选择（因变量）只有两个：留（Y）/不留（N），而并非如工资水平这样的连续因变量有无限个值。一般地，对于因变量是二元变量的回归问题，则可以用逻辑回归模型进行分析（图2）。

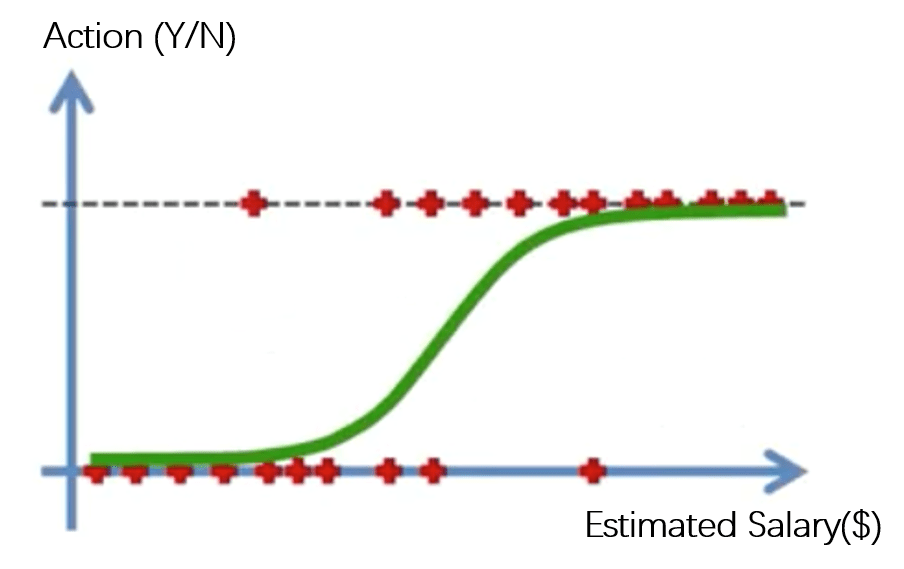
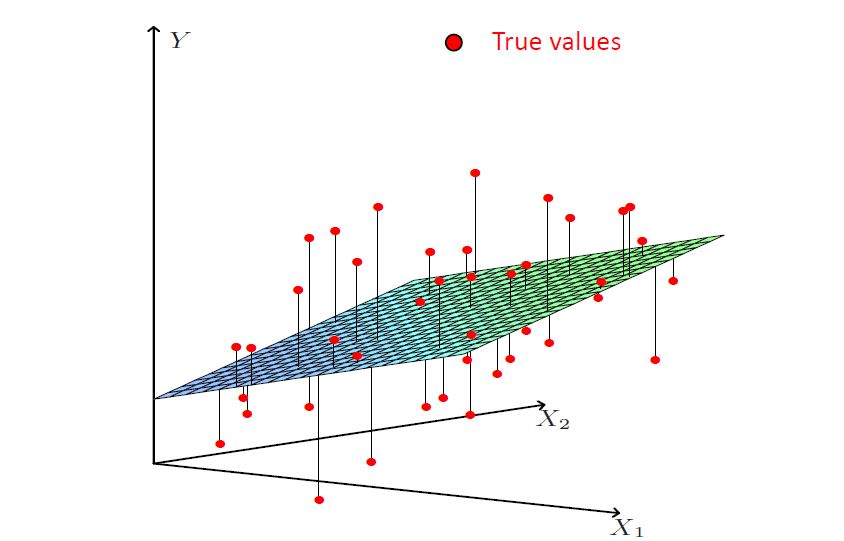
实际上，回归模型多种多样，在上文提及的几种回归模型以外，还有诸如线性回归的特殊形式：Polynomial回归；加入参数惩罚（正则化）的线性回归：Ridge回归、Lasso回归、ElasticNet回归；逻辑回归的泛化形式：softmax回归等等。此外，要更加系统地讨论回归，除了讨论不同回归模型的特征外，最优化模型的参数估计也是值得研究的方面。因此，本文仅作为探讨回归问题的始端，以期能在接下来的几个月里对一些主流的回归模型和参数估计方法逐个地进行整理和思考。